Chomp

We shall together play a game by chomping on a bar of chocolate, with a game-theoretic surprise, by which one player steals the strategy of another.

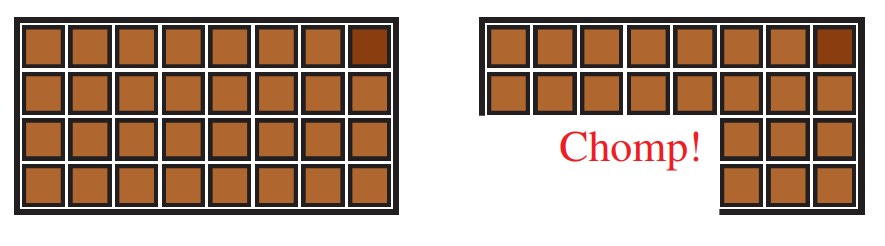
Consider next the game of Chomp, in which two players have turns taking bites from a delicious bar of chocolate. We consider an n × m rectangular chocolate bar, consisting of small chocolate squares.

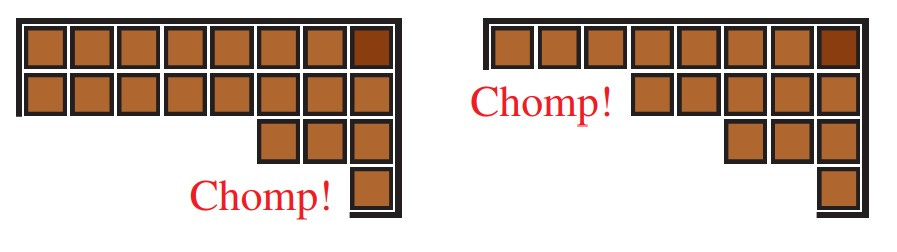
According to the rules of the game, the players will “chomp” the bar always from the lower left, selecting on each move a particular square in the bar and removing it along with the rest of the bar below and to the left of that square. The player who chomps the very last highlighted square at the upper right loses.

Who will win? Would you rather go first or second? Does this decision depend on the size of the initial chocolate bar? What will the winning moves be?

Interlude

Please enjoy this selection from Infinite Games: Frivolities of the Gods, my new book serialized here with fresh material on games and the logic of games each week.

This week we look into the game of Chomp!

Have you decided whether to go first or second? Let us get into the analysis.