Face Up

How long is the longest play of the game? Can you play forever, avoiding the terminal all-face-up position?

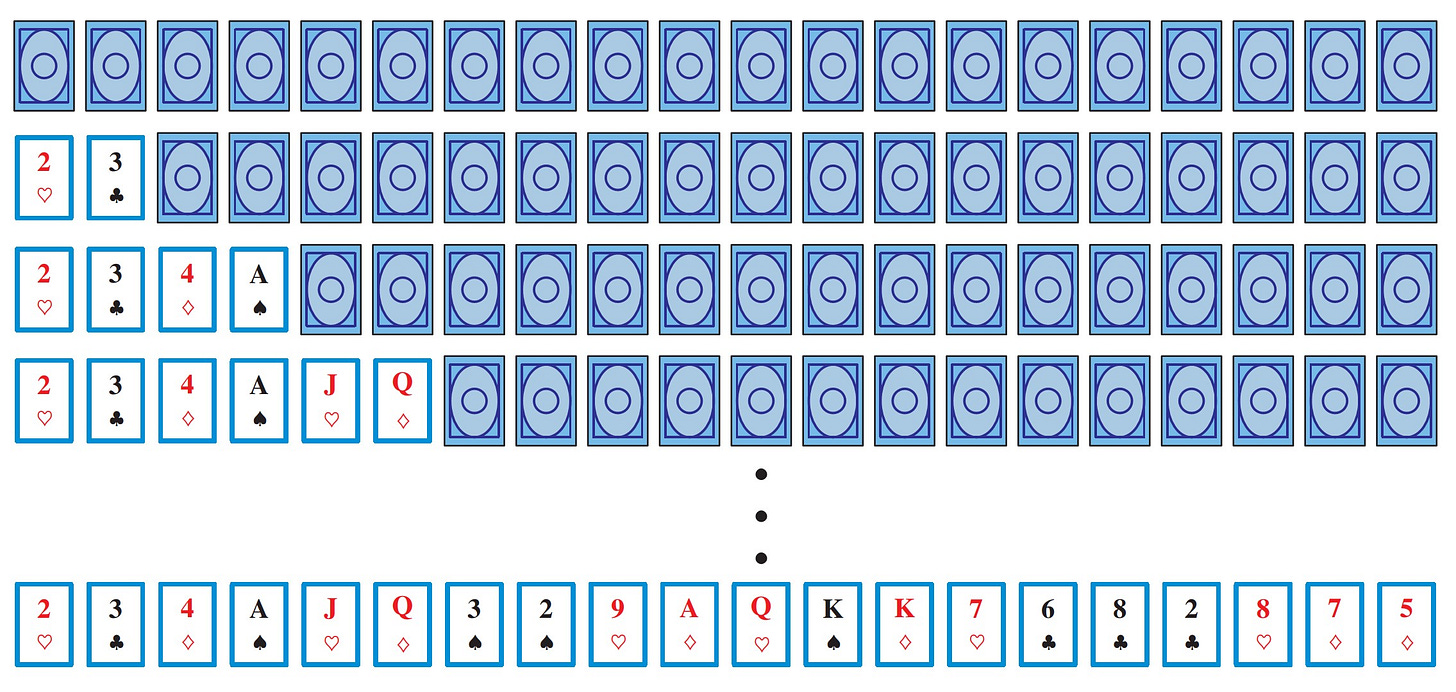
In this post and the next several posts coming, I should like to show you several interesting sequence games, beginning with the simple solitaire game I call Face Up, played with twenty random cards placed face down in a row.

A move in the game consists of turning a face-down card face up, and then turning over the card immediately to the right, if any. Perhaps play begins like this:

The question I should like to ask, when undertaking a sequence of such moves, is whether one can play so as to avoid the terminal position with all cards being face up—that would mean the end of the game, with no further moves possible. Can we avoid it? In other words, is there an endless play?

Interlude

One can easily force a quick resolution of the Face Up game, of course—simply turn over the first two cards, and then the next two, and so forth. In this way we turn all the cards face up in ten moves.

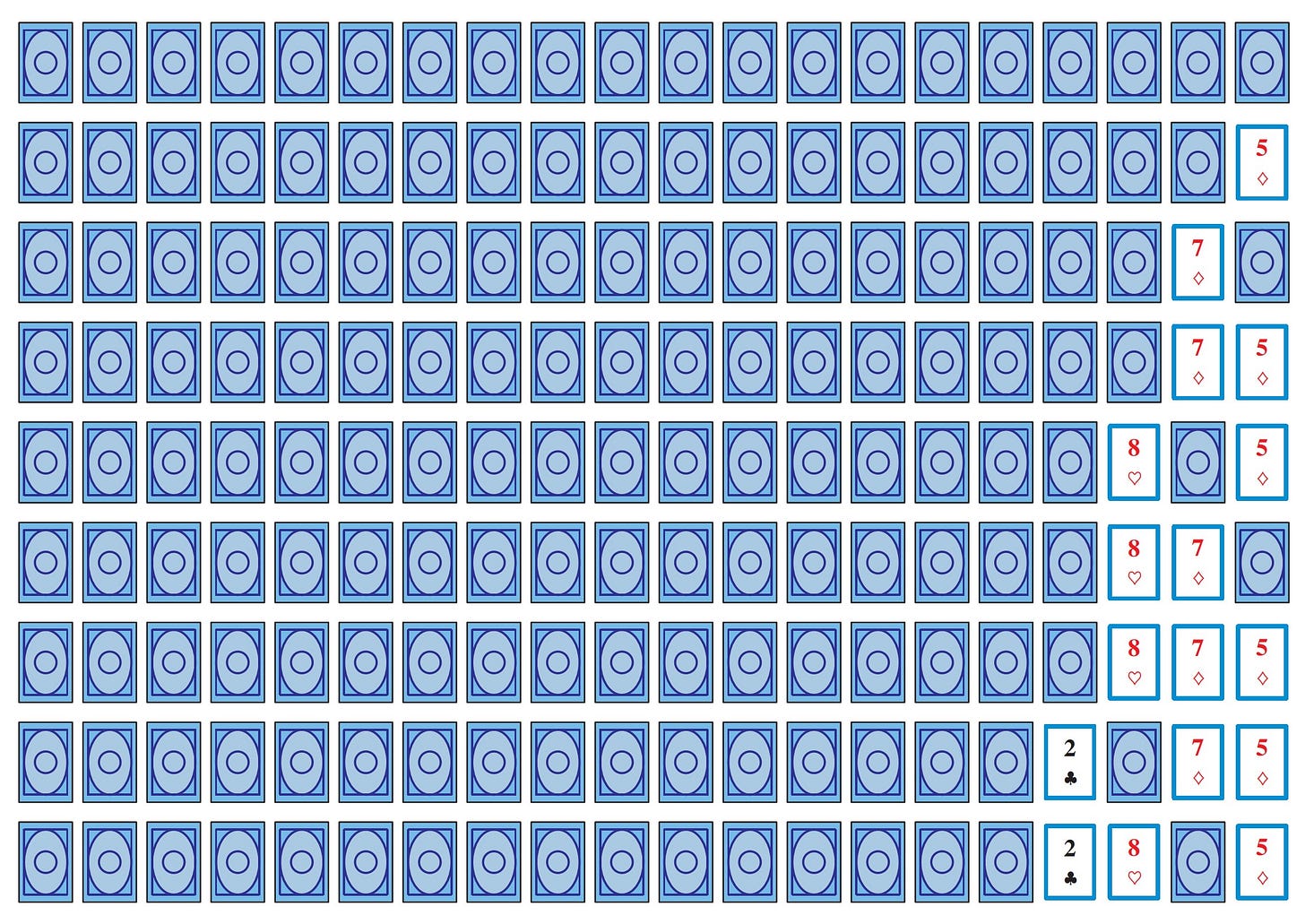
With this strategy, we act always upon the left-most face-down card, leading to the all-face-up position in a number of moves equal to half the number of cards (rounded up), which is clearly as quickly as possible, since every move creates at most two new face up cards. Meanwhile, other ways of playing the game exhibit much longer play. Consider the policy that acts instead always upon the right-most face-down card.

Notice how the moves in effect create an increasing region of face-up cards at the right, with each next face-down card in effect sliding through it off to the right.

Can we make a longer play? Can we achieve endless play? Since there are only finitely many possible configurations of the cards with respect to being face down or face up, any infinite sequence of moves would have to repeat a configuration, and clearly if we can ever find a position that comes back to itself, then we could simply repeat this process and thereby achieve an infinite play. So another way to ask the question is whether one can ever undertake a sequence of moves from a position in such a way so as to come back to that same position. Is it possible?

Interlude

There are no infinite plays

The answer is no, and in fact no matter how one applies the moves, one will inevitably reach the terminal all-face-up position in finitely many moves. One way to see this is to think of the face-down cards as representing the number 1 and face-up as 0. The original sequence of cards is thus associated with the sequence 11111111111111111111, and the position at some other stage of play might be something like 11010001101001110010. We may think of these binary sequences as the binary representation of a natural number. Each move in Face Up consists of turning some digit 1 to 0, and then flipping the bit immediately to the right, if any. Thus, we turn 11 into 00 and 10 into 01. Or, in the special case that we act on the final 1, then we simply turn it to 0.

\(\begin{align*}\Large 110{\color{Red}\mathbf{10}}\kern.5pt001101001110010 & \\ \Large 110\kern.5pt{\color{Red}01}001101001{\color{Red}\mathbf{11}}0010 & \quad {\LARGE\downarrow} \\ \Large 11010001101001{\color{Red}00}\kern.5pt0010 & \\ \end{align*} \)

The key observation is that such an action on binary digits always makes the corresponding number strictly smaller. We are reducing a higher-place digit from 1 to 0 and then changing only a lower-place digit, which inevitably reduces the value. Since these numbers are therefore descending in the natural numbers, it follows that the process must eventually come to a halt (there will be no negative numbers arising here). The only way the process can stop, however, is when we have all zeros and therefore no possibility to act further. So every sequence of moves must eventually terminate in the all-face-up position.

This argument made a nice appearance in the film X+Y about a young math prodigy.

An upper bound on the length of play

Let us try to extract more information from the argument. In fact we can use it to provide a natural upper bound on the longest possible length of play. Namely, we argued that every position with n cards corresponds to a number with n binary digits, which descend during play. Since the largest such number, with all digits being one 1111111, has value 2ⁿ - 1, it follows that we shall hit zero in at most 2ⁿ - 1 steps.

With 20 cards, this argument shows that every sequence of moves will terminate in the all-face-up position in at most 2²⁰ - 1 steps, which is 1048575 steps, a little over a million. Is this bound optimal? If we made a move in the game every second, this would take about twelve days of continuous play. Can we really play so long?

Interlude

The optimal bound—the longest play

No, it turns out that we cannot actually play for such a long time. In fact, the correct value of the longest play with twenty cards is merely 210 steps. The game inevitably finishes, therefore, in a matter of minutes rather than twelve days of furious continuous play as calculated by our earlier bound. In the general case of Face Up starting with n face-down cards, what I claim is that the longest play has exactly

\(1+2+\cdots+n\)

moves, which is n(n+1)/2. Thus, the growth rate is merely quadratic in the number of cards, rather than exponential as in the previous bound.

To see this, let me prove a somewhat sharper claim, namely, that for any pattern of cards with binary sequence s, the longest play will have exactly

\(\sum_{s_k=1}k \)

many moves, with a term for each appearance of digit 1 in s. Let me call this number the position sum of s, since it is the sum of the digit positions of the 1 digits in s.

First, we may observe that indeed there is such a play on s of this length. Namely, by acting always on the right-most face-down card, in the style described above, we shall achieve the position sum. We had noticed that this strategy has the effect of moving the right-most face-down card to the right one place and eventually off the board, and since this takes k moves for a face-down card in position k, it follows that the method overall will terminate in

\(\sum_{s_k=1}k\)

steps, which contributes value k whenever there is a face-down card in position k. So the position sum is exactly realized by this manner of play.

Conversely, let me prove by induction that all possible plays on a card sequence with pattern s will end by the position sum. Any action will in effect turn some 10 into 01 or some 11 into 00. In both cases, the resulting position sum is strictly lower by at least one, and therefore, by the induction hypotheses, the resulting sequences will last for at most their position sum. And so it is also true for s.

With n cards, the largest position sum occurs when all the digits are one, 1111111, which corresponds to the starting all-face-down position. The position sum in this case is

\( 1+2+\cdots+n,\)

which is n(n+1)/2. So this is the longest possible length of play in Face Up.

I would like especially to call the reader's attention to the fact that the longest play we described above, acting always upon the right-most face-down card, always uses 10 ↦ 01 and never 11 ↦ 00, which I find interesting because this is exactly preserving the position sum as large as possible.

A variation

Let us consider a variation of the Face Up process, by which any face down card can be turned face up, and then cards to the right can be adjusted however one likes. How does this affect the analysis?

Interlude

The game still has finite length, by induction on the position of the left-most face-down card. If we never act upon it, then by the induction hypothesis all the cards to the right of it will eventually become face up, at which point, we will have to act upon that card. But at this point, we reduce immediately to the smaller case, since now the left-most face-down card has a lower position. The reader is invited in the questions for further thought to investigate the length of the longest play in this variation of the Face Up process.

Questions for Further Thought

1. Is every pattern of twenty cards, face down or and face up accordingly, realizable in Face Up from the initial position of all face down cards? If not, can you provide a particular pattern that is impossible? Can you say anything general about the patterns that are or are not realizable?

2. We saw that from the all-face-down position the Face Up strategy of acting always upon the left-most face-down card was very quick, while the strategy of acting upon the right-most face-down card was comparatively slower. Is there a starting position that reverses this situation? Are there positions where the two methods take the same amount of time? Can you identify exactly which positions for which the act-upon-left-most strategy always takes the longest possible time?

3. What is the longest play from the starting position with 20 cards in the Face Up variation in which one can turn a face-down card face up and then make arbitrary changes to the right? With n cards, how long is the longest play?

Credits

An account of what I call the Face Up game appears in the film X+Y about a young maths star.

Coming soon

Stay tuned for coming posts on other simple sequence games, including the Bubble Monsters, as well as Pushpast and Pushthrough.