The game of Nim

We shall study the classic game of Nim, learning the secret mathematical strategy that will enable you to win against those who don’t yet know the secret.

The game of Nim is a mathematician’s delight. The winning strategy is fundamentally mathematical, with just the right level of complexity so that a person can enjoyably implement it in actual games, but difficult enough so that an opponent who does not know the strategy is unlikely to play reliably in accordance with it. Those in the know can therefore usually expect to win—nearly every time—against those who do not know the strategy, even when starting from a random or losing position. I have taught children the strategy, who then go on to defeat adults systematically. What fun!

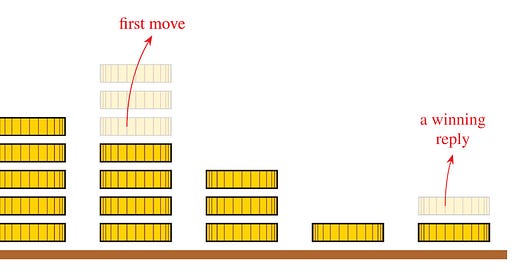
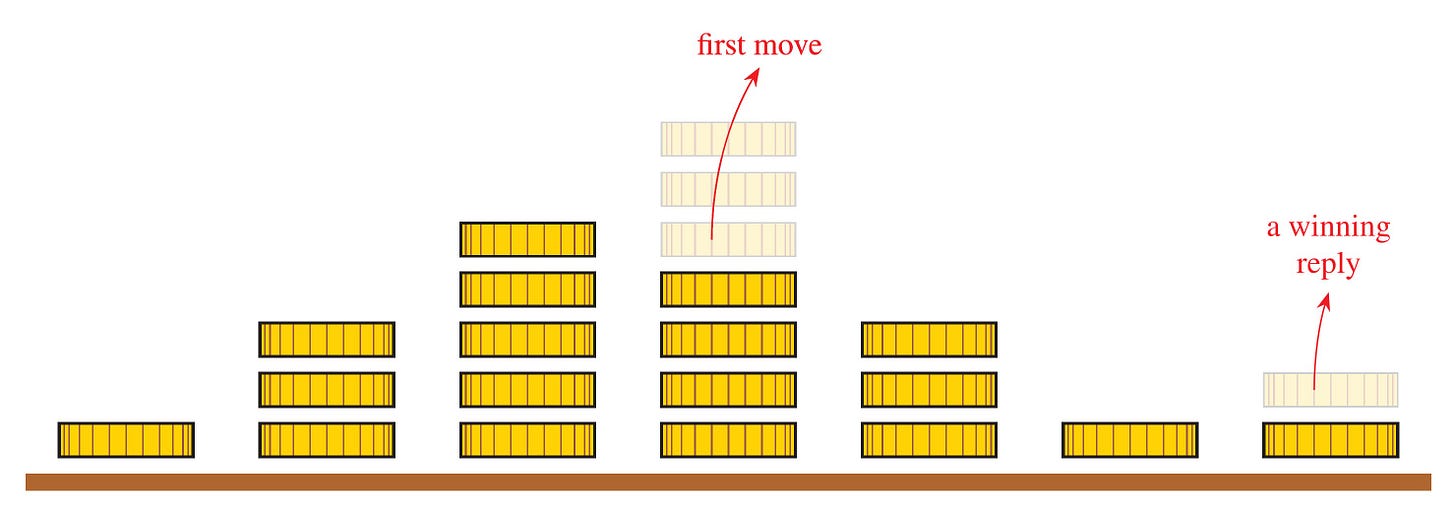
To play Nim, one player sets up finitely many piles of coins and the other decides whether to move first or second. On each turn, a player removes one or more coins from any one pile—take one coin, two coins, or even the entire pile, as you like. Whoever takes the very last coin overall wins the game.

Can you discover the secret winning strategy?

Interlude

Please enjoy this selection from Infinite Games: Frivolities of the Gods, my new book serialized here with fresh material on games and the logic of games each week.

This week we look into the game of Nim!

Let’s get into it—a complete account of Nim. We’ll start with first-grader Nim, an easier case that is still challenging for adults, and yet first-graders can learn the strategy, before working up to the fully general winning strategy for Nim. Afterwards, we shall also solve Misère Nim.