Logicism

Aiming to reduce all mathematics, including the concept of number, to logic

This is a selection from chapter 1 of my book, Lectures on the Philosophy of Mathematics, MIT Press 2021. I used this text as the basis of my lecture series over several years in Oxford. An introduction to the philosophy of mathematics, with an approach grounded in mathematics—one in which the philosophical issues arise organically from mathematical considerations.

Lectures on the Philosophy of Mathematics, MIT Press 2021

Logicism

Pursuing the philosophical program known as logicism, Gottlob Frege, and later Bertrand Russell and others at the dawn of the twentieth century, aimed to reduce all mathematics, including the concept of number, to logic. Frege begins by analyzing what it means to say that there are a certain number of things of a certain kind. There are exactly two things with property P, for example, when there is a thing x with that property and there is another distinct thing y with that property, and furthermore, anything with the property is either x or y. In logical notation, therefore, “There are exactly two Ps” can be expressed like this:

\( \exists x,y\ \bigl(\textup{P}x∧ \textup{P}y∧ x\neq y∧ \forall z(\textup{P}z\to z=x∨ z=y)\bigr). \)

The quantifier symbol ∃ is read as “There exists” and ∀ as “For all,” while ∧ and ∨ mean “and” and “or,” and → means “implies.” In this way, Frege has expressed the concept of the number 2 in purely logical terms. You can have two sheep or two apples or two hands, and the thing that is common between these situations is what the number 2 is.

Equinumerosity

Frege's approach to cardinal numbers via logic has the effect that classes placed in a one-to-one correspondence with each other will fulfill exactly the same Fregean number assertions, because the details of the truth assertion transfer through the correspondence from one class to the other. Frege's approach, therefore, is deeply connected with the equinumerosity relation, a concept aiming to express the idea that two sets or classes have the same cardinal size. Equinumerosity also lies at the core of Georg Cantor's analysis of cardinality, particularly the infinite cardinalities discussed in a later chapter.

Specifically, two classes of objects (or as Frege would say: two concepts) are equinumerous—they have the same cardinal size—when they can be placed into a one-to-one correspondence. Each object in the first class is associated with a unique object in the second class and conversely, like the shepherd counting his sheep off on his fingers.

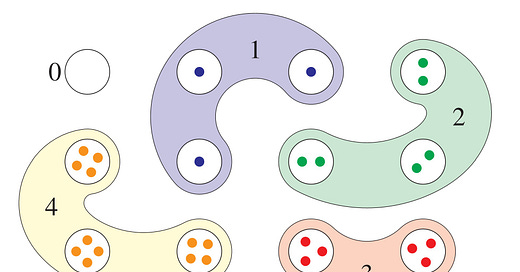
So let us consider the equinumerosity relation on the collection of all sets. Amongst the sets pictured here, for example, equinumerosity is indicated by color: all the green sets are equinumerous, with two elements, and all the red sets are equinumerous, and the orange sets, and so on.

In this way, equinumerosity enables us systematically to compare any two sets and determine whether they have the same cardinal size.

The Cantor-Hume principle

At the center of Frege's treatment of cardinal numbers, therefore, is the following criterion for number identity:

Cantor-Hume principle. Two concepts have the same number if and only if those concepts can be placed in a one-to-one correspondence.

In other words, the number of objects with property P is the same as the number of objects with property Q exactly when there is a one-to-one correspondence between the class { x | P(x) } and the class { x | Q(x) }. Expressed in symbols, the principle asserts

\(\#\textup{P}=\#\textup{Q}\qquad\textup{ if and only if }\qquad\{\ x\mid \textup{P}(x)\ \}\quad\simeq\quad\{\ x\mid \textup{Q}(x)\ \},\)

where #P and #Q denote the number of objects with property P or Q, respectively, and the symbol ≃ denotes the equinumerosity relation.

The Cantor-Hume principle is also widely known simply as Hume's principle, in light of Hume's brief statement of it in A Treatise of Human Nature (1739, I.III.I), which Frege mentions (the relevant Hume quotation appears in a later chapter). Much earlier, Galileo mounted an extended discussion of equinumerosity in his Dialogues Concerning Two New Sciences (1638), considering it as a criterion of size identity, particularly in the confounding case of infinite collections, including the paradoxical observation that line segments of different lengths and circles of different radii are nevertheless equinumerous as collections of points. Meanwhile, to my way of thinking, the principle is chiefly to be associated with Cantor, who takes it as the core motivation underlying his foundational development of cardinality, perhaps the most successful and influential, and the first finally to be clear on the nature of countable and uncountable cardinalities. Cantor treats equinumerosity in his seminal set-theoretic article, Über eine Eigenschaft des Inbegriffs aller reelen algebraischen Zahlen (1874), and states a version of the Cantor-Hume principle in the opening sentence of Ein Beitrag zur Mannigfaltigkeitslehre (1878). In an 1877 letter to Richard Dedekind, he proved the equinumerosity of the unit interval with the square, the cube, and indeed the unit hypercube in any finite dimension, saying of the discovery, “I see it, but I don't believe it!” We shall return to this example in a later section.

The Cantor-Hume principle provides a criterion of number identity, a criterion for determining when two concepts have the same number. Yet it expresses on its face merely a necessary feature of the number concept, rather than identifying fully what numbers are. Namely, the principle tells us that numbers are classification invariants of the equinumerosity relation. A classification invariant of an equivalence relation is a labeling of the objects in the domain of the relation, such that equivalent objects get the same label and inequivalent objects get different labels. For example, if we affix labels to all the apples we have picked, with a different color for each day of picking, then the color of the label will be an invariant for the picked-on-the-same-day-as relation on these apples. But there are many other invariants; we could have written the date on the labels, encoded it in a bar code, or we could simply have placed each day's apples into a different bushel.

The Cantor-Hume principle tells us that numbers—whatever they are—are assigned to every class in such a way that equinumerous classes get the same number and nonequinumerous classes get different numbers. And this is precisely what it means for numbers to be a classification invariant of the equinumerosity relation. But ultimately, what are these “number” objects that get assigned to the sets? The Cantor-Hume principle does not say.

The Julius Caesar problem

Frege had sought in his logicist program an eliminative definition of number, for which numbers would be defined in terms of other specific concepts. Since the Cantor-Hume principle does not tell us what numbers are, he ultimately found it unsatisfactory to base a number concept solely upon it. Putting the issue boldly, he proclaimed

we can never—to take a crude example—decide by means of our definitions whether any concept has the number Julius Caesar belonging to it, or whether that same familiar conqueror of Gaul is a number or not.

Frege, Foundations of arithmetic (1884)

The objection is that although the Cantor-Hume principle provides a number identity criterion for identities of the form

\(\#P = \#Q,\)

comparing the numbers of two classes, it does not provide an identity criterion for identities of the form

\(\#P = x,\)

which would tell us which objects x were numbers, including the case

\(\#P = \text{Julius Caesar}.\)

On its face, this objection is strongly antistructuralist, a position we shall discuss at length in a later section, for it is concerned with what the numbers are, rather than with their structural features and roles. Yet, Greimann (2003) and others argue, nevertheless, that there is a nuanced structuralism in Frege.

Numbers as equinumerosity classes

In order to define a concept of number suitable for his program, Frege undertakes a process of abstraction from the equinumerosity relation. He realizes ultimately that the equinumerosity classes themselves can serve as numbers.

Specifically, Frege defines the cardinal “number” of a concept P to be the concept of being equinumerous with P. In other words, the cardinal number of a set is the class of all sets equinumerous with it, the equinumerosity class of the set:

\( \#P\qquad =_{\text{def}} \qquad \{\ x\mid x\simeq P\ \}. \)

For Frege, the number 2 is the class of all two-element collections; the number 3 is the class of all three-element collections, and so on. The number 0 is precisely {∅}, since only the empty set has no elements. Frege's definition fulfills the Cantor-Hume principle because sets have the same equinumerosity class if and only if they are equinumerous.

Frege proceeds to develop his arithmetic theory, defining zero as the cardinal of the empty class and defining that a number m is the successor cardinal of another n if m is the cardinal of a set obtained by adding one new element to a set of cardinal n; the natural numbers are the cardinals generated from 0 by successive applications of the successor operation, or more precisely, the numbers having every property of 0 that also is passed from every cardinal to its successor. If one regards equinumerosity and these other notions as logical, then this approach seems ultimately to reduce arithmetic to logic.

At first independently of Frege, but later responding to and building upon Frege's work, Bertrand Russell also sought to found mathematics in logic. Russell was impressed by Peano’s (1889) formalization of arithmetic, but he viewed Frege's foundation as still deeper in providing purely logical accounts of the arithmetic notions of “zero,” “successor,” and “natural number.” In their subsequent monumental work, Principia Mathematica, Russell and Alfred North Whitehead wove both themes into their account of arithmetic.

Neologicism

The logicist programs of Frege and Russell came widely to be viewed as ultimately unsuccessful in their attempts to reduce mathematics to logic. Frege's foundational system was proved inconsistent by the Russell paradox (discussed in a later chapter), and Russell's system is viewed as making nonlogical existence assertions with the axiom of infinity and the axiom of choice. Nevertheless, logicism is revived by Bob Hale and Crispin Wright and others in the neologicist program, reconstruing Frege's approach to logicism in a way that avoids the pitfall of inconsistency, aiming once again to reduce mathematics to logic.

Specifically, Frege’s Conception of Numbers as Objects (Wright 1983) aims to found Frege's arithmetic directly upon the Cantor-Hume principle, establishing the Peano axioms without need for the problematic foundational system. Equinumerosity, expressed in second-order logic, is taken as logical. (Some philosophers object at this point, regarding second-order principles as inherently set-theoretic and mathematical, but let us proceed with the neologicist perspective.) The neologicists address the Julius Caesar problem by seeking a purely logical account of the number-assignment problem, building upon suggestions of Frege regarding the process of abstraction. Frege explains, for example, how we refer to the direction of a line, having initially only a criterion of same-directionality, namely, parallelism. Similarly, we might speak of the order of a sequence of chess moves, or the pattern of an arrangement of colored tiles, or perhaps the value of a certain item. In each case, we refer to an abstract entity with a functional expression f, defined only implicitly by a criterion of the form

\( f(a)=f(b)\quad\textup{ if and only if }\quad Rab, \)

with an equivalence relation R. The direction of line ℓ₁ is the same as the direction of line ℓ₂, for example, exactly when ℓ₁ is parallel to ℓ₂; one tiling pattern is the same as another if the tiles can be associated to match color and adjacency from one arrangement to the other. The Fregean process of abstraction takes such an abstraction principle to define an abstract function f. The main point, of course, is that the Cantor-Hume principle itself is such an abstraction principle, where we refer to the number of elements in a class, and two classes have the same number if and only if the classes are equinumerous. By the process of abstraction, we therefore achieve numbers as abstract objects.

Meanwhile, there are logical problems with taking every abstraction principle as legitimate, as some of them lead to inconsistency. The general comprehension principle, for example, can arise via Fregean abstraction. Thus, the principle of abstraction is said to consort with “bad company”; known-to-be-false principles arise as instances of it. This is merely a gentle way of saying, of course, that abstraction is wrong as a principle of functional definition. We do not usually say that the fallacy of denying the antecedent consorts with “bad company” because it has false instances; rather, we say that it is fallacious.

One last thing: here you can jump into the middle of one of my Oxford lectures on YouTube, where I discuss the topic of logicism:

Available on Amazon