Mutual and bi-interpretation of models

When two models each interpret the other, we may follow the interpretations back and forth between them, finding ourselves thereby amidst a fractal pattern of nested interpretations

In recent posts, we have been discussing the topic of interpretation in mathematics, which occurs when we can find a definable copy of one mathematical structure within another. Having done so, we saw how the interpretation translation allows one to express all the truths of the first model entirely in terms of the language and structural features of the second.

In this post, we shall explore the situation arising when we can also interpret the second model conversely inside the first—each model is interpreted in the other.

Enjoy this installment from A Panorama of Logic, an introduction to topics in logic for philosophers, mathematicians, and computer scientists. Fresh content each week.

This is the third in a series of posts on interpretability.

Please consider subscribing as a free or paid subscriber.

Mutual interpretation

Two structures are said to be mutually interpretable when each of them is interpretable in the other.

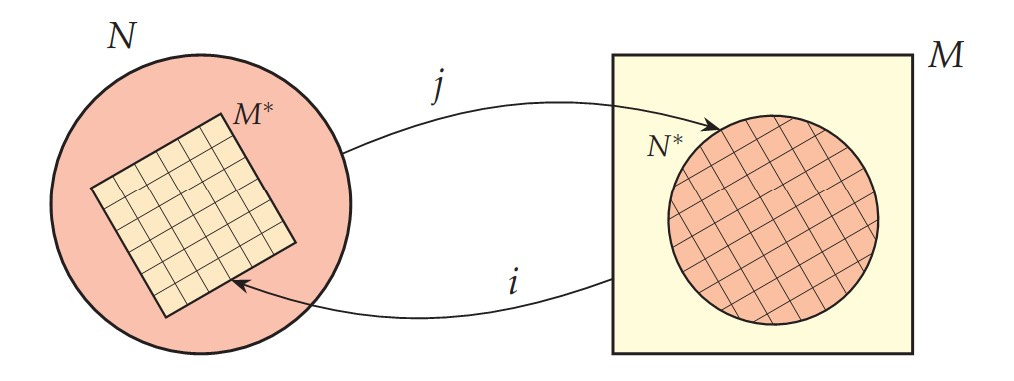
Inside each of them, we can define a definable copy of the other structure, using a definable class of k-tuples with definable atomic structure and a definable congruence relation, so that the interpreted model is isomorphic to the quotient of that definable structure. The model N is isomorphic via j to the model N* definable inside M, and M is isomorphic via i to M* defined inside N.

(Stay tuned for the notion of bi-interpretability, a strictly stronger notion.)