Tic tac toe and variants

We consider various game-theoretic aspects of several variations of the school-child game of tic-tac-toe, including 4 × 4 tic-tac-toe, recursive tic-tac-toe, and 3D tic-tac-toe.

The familiar game of tic-tac-toe, or noughts and crosses, is played by school children everywhere. The players take turns placing X or O respectively on a 3 × 3 grid, and whichever player first achieves three-in-a-row on any row, column, or diagonal is the winner—they made tic-tac-toe.

The game is famously a draw with optimal play—either player can ensure that their opponent fails to achieve tic-tac-toe. In the exhibition game play above, which was a win for X and not a draw, player O made a mistake in his opening move—he should have played O on a corner square instead of the edge as he did. The subsequent moves by X took advantage of the mistake with forcing moves to set up the double tic-tac-toe threat, thereby ensuring the X win. In fact, there were many winning lines for X after O's initial blunder.

Perhaps we all know from experience that tic-tac-toe is a draw with optimal play, but how could one prove it? The only proofs I know, unfortunately, are detailed case arguments, exhaustively exploring the space of possible play. For example, this xkcd cartoon details a complete drawing strategy for each player, in what I find to be a startlingly effective presentation of the strategy and the game tree.

While I don't know of any truly soft proof that tic-tac-toe is a draw, I do know some soft arguments for related, if weaker, conclusions, and so let us discuss one of those arguments.

No winning second–player strategy

First, I shall offer a soft strategy-stealing argument that the second player can have no winning strategy in tic-tac-toe. To see this, we suppose toward contradiction that the second player does have a winning strategy in tic-tac-toe. Call this strategy σ, a procedure telling player two how to mark the board in any given situation, such that if we follow the instructions as player two, we are guaranteed to win.

We shall play as player one, while aiming to “steal” the winning strategy σ. It doesn't make sense directly to consult σ about how to play as player one, since it is a winning strategy for player two, which is guaranteed to play well only when consulted for player-two moves.

Rather, the strategy-stealing idea is that we shall somehow pretend to be player two. Playing as player one in the actual game, we shall simply invent an imaginary first move for our opponent. It doesn't even matter where—let us imagine that they had opened with a move in the center square. The effect is that we are playing as player two in this imaginary game with the extra move, and so we may consult the winning strategy σ about how to play. We proceed to make exactly those moves in the actual game, and so except for the supplemental imaginary move, the two games are identical. A minor issue is that if in the actual game our opponent should happen later actually to play the imaginary move we had already assigned to them, then it is no problem, for we can simply invent a different imaginary move for them at this point, and continue consulting σ. (We don’t change the original first move or the imaginary game history, but rather invent a new imaginary move for them to play in the imaginary game on this turn.)

The main point is that because we had assumed that σ is a winning strategy for player two and we are playing according to σ as player two in the imaginary game, it means that we will achieve tic-tac-toe in the imaginary game before the opponent does so. But since we had made those same moves in the actual game, and all our opponent's actual moves appear in the imaginary game, it means that we will have achieved tic-tac-toe also in the actual game before our opponent. Thus, we have described how to provide a winning strategy for player one.

But this is impossible, a contradiction, since it cannot be that both players have winning strategies. So therefore, it cannot be that player two has a winning strategy in tic-tac-toe, which is what I claimed.

4 × 4 tic-tac-toe

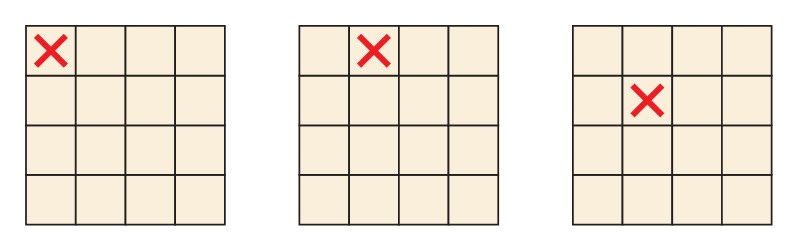
Let us consider the variant of tic-tac-toe played instead on a 4 × 4 board, with each player trying to get four-in-a-row on any row, column, or diagonal. We might naturally call the game, “tic tac tip toe.” Perhaps the game play begins like this:

Did they play well? Do you think either player can have a winning strategy in 4 × 4 tic-tac-toe?

No advantage going second

There is no advantage, I claim, to going second in 4 × 4 tic-tac-toe. Perhaps this seems obvious—how could it ever help us to allow the opponent a first move? But I should like to give a careful argument. We shall mount another strategy-stealing argument, just as we did for 3 × 3 tic-tac-toe. What I claim is that if player two has a winning or even a drawing strategy, then player one has such a strategy as well. Therefore, in fact player two cannot have a winning strategy, since it can't be that both players have winning strategies.

The argument is this. If player two had a winning strategy in 4 × 4 tic-tac-toe, then we as player one in an actual game can simply pretend to be player two. We invent an imaginary first move for our opponent, and thereafter play according to the player-two winning strategy. If our opponent should ever happen actually to play the imaginary move we had already attributed to them, we can simply invent another imaginary move at that moment and continue.

The main point, as before, is that because we are playing according to the supposed winning strategy in the imaginary game, we will win that game, achieving a 4 × 4 tic-tac-toe before our opponent does. It follows that we achieve this also in the actual game, since we have made the same moves in both games, and our opponent as well, except that the invented moves for them in the imaginary game will not all be present for them in the actual game. In short, any winning strategy for the second player can by this method be turned into a winning strategy for the first player. But since they cannot both have winning strategies, this would be a contradiction, if it occurred, and so there must be no winning strategy for the second player to begin with.

Applied with drawing strategies instead of winning strategies, the strategy-stealing argument shows that if player two has a drawing strategy, then so does player one. So the situation is that either player one can force a win, or both players have drawing strategies.

How many opening moves up to symmetry?

I would like to count the number of opening moves in 4 × 4 tic-tac-toe. The board has sixteen squares in total, of course, and so there are plainly sixteen possible different opening moves for player X.

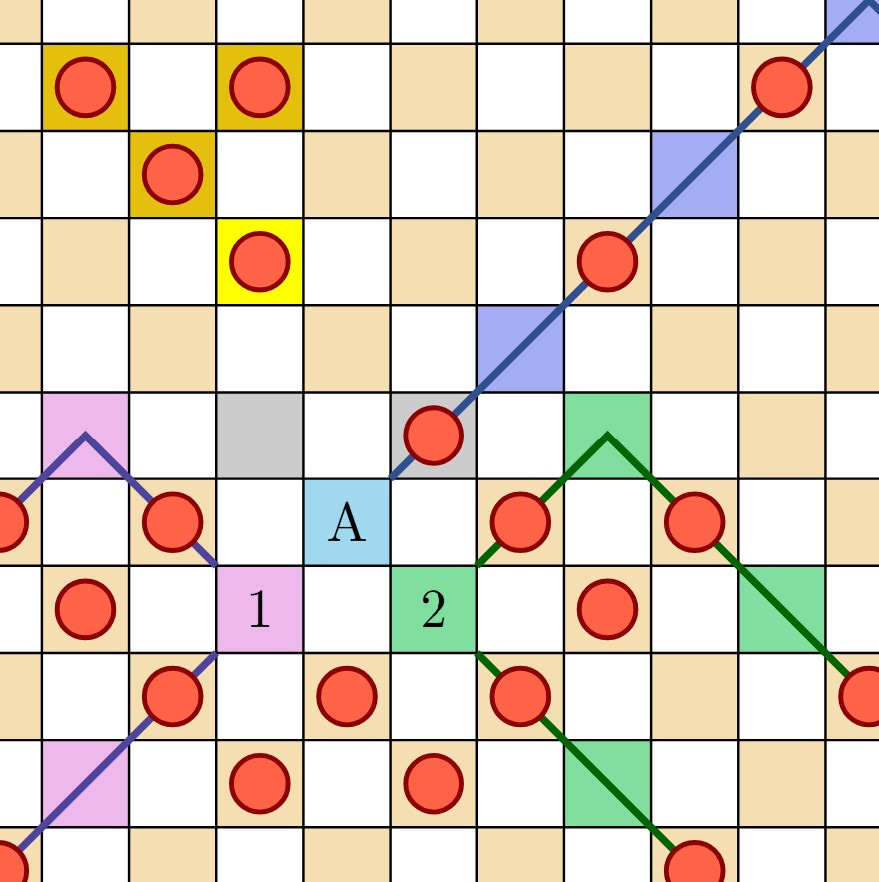
But the board exhibits many symmetries, which make many of these moves essentially equivalent to one another from the point of view of strategic analysis. For example, all the corner moves are essentially equivalent, since if you make an opening move in any corner, I can rotate the board (or rotate merely how I view the board) so as to move that particular corner square to the upper left corner. And since rotating the board does not affect any strategic or game-theoretic consideration, it follows that all opening corner moves are strategically identical. Similarly, any opening move on a corner-adjacent edge square can be moved to any other by rotating and reflecting the board as necessary. And finally the four center squares can similarly be moved to each other by rotation. Up to these rigid symmetries of the square, therefore, there are only three possible opening moves, as indicated here:

Let me argue further, however, that there are actually only TWO opening moves in 4 × 4 tic-tac-toe up to strategic equivalence. What I claim is that the corner squares and the center squares play identical strategic roles in the game. Really? Yes! The fact of the matter is that there is a deeper symmetry of the board, one which does not arise by rigid rotation or reflection, but which nevertheless swaps the corners with the center while preserving all the winning tic-tac-toe lines. Surprising though it may seem, this symmetry thereby shows that opening with a corner play is strategically identical to opening in the center.

Let me explain.

Please enjoy this selection from Infinite Games: Frivolities of the Gods, my new book serialized here with fresh material on games and the logic of games each week.

This week we look into variations of tic-tac-toe, including 4x4 tic-tac-toe, recursive tic-tac-toe, 3D tic-tac-toe, and more.