The zigzag theorem

A selection from Proof and the Art of Mathematics

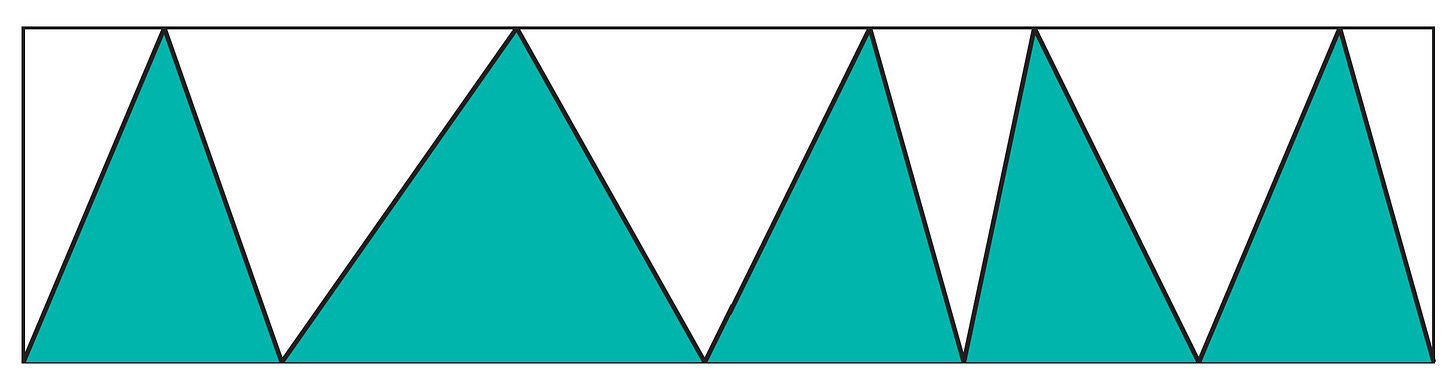
Let us conclude with a fun observation that I call the zigzag theorem. Consider any rectangle, and draw a zigzag pattern in it, moving back and forth from the bottom edge to the top along straight lines, as many times as you like but without crossing your own lines.

This forms a number of triangles. What proportion of area is in the triangles below the zigzag pattern?

This is a brief excerpt from my book Proof and the Art of Mathematics, an introduction to the art and craft of proof-writing for aspiring mathematicians who want to learn how to write proofs. Compelling mathematical statements with interesting, elementary proofs.

Proof and the Art of Mathematics has been awarded the 2024 Daniel Solow Author’s Award by the Mathematical Association of America, awarded for outstanding and impactful contributions to mathematics education.

Theorem. The triangles formed by any zigzag pattern in a rectangle carve out exactly half the area of the rectangle.

Proof: We assume at first in this proof that the zigzag pattern never doubles back, so that the zigzag path proceeds steadily to the right. In this case, all the triangles have acute base angles, and the vertex of each triangle occurs above its base. Let us construct a vertical line on each vertex used in the zigzag pattern. This carves the rectangle into smaller rectangles, as illustrated below, and the main point is that each such rectangle is cut exactly in half diagonally by the corresponding zig or zag across the rectangle.

Thus, exactly half the area of the rectangle is above the zigzag and half below, as desired. This proves the theorem for the acute-triangle case.

Let us now drop the no-doubling-back assumption and consider the general case, where we allow zigzag patterns that sometimes move backward (but not crossing themselves), like this:

This kind of case breaks the previous proof, because the constructed rectangles would overlap. Nevertheless, we can mount an alternative argument. The point is that if the original rectangle has width w and height h, then each triangle has height h and thus area ½bh, where b is the base of that triangle. Since the triangle bases add up to the total width w, it follows that the sum of the areas of the triangles is ½wh, which is exactly half the area of the rectangle, as desired. □

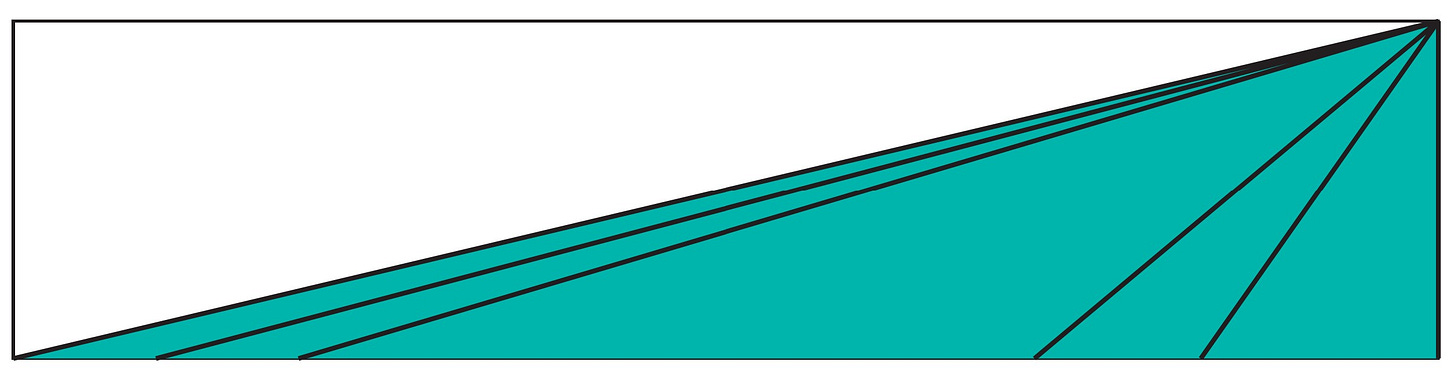
Alternative proof: Another way for us to argue in the general case is to observe that moving the top vertices of the triangles along the top edge of the rectangle is an area-preserving transformation because it preserves the base and height of each triangle. We can transform the skewed-triangle zigzags to the acute-triangle case, for example, simply by moving the top vertex of every triangle to be above its base. More directly, however, let us simply combine all the triangles into one by moving their top vertices all the way to the right like this:

After this transformation, they form the region below the diagonal of the rectangle, which is exactly half the area. Since the transformation is area preserving, the original triangles must also have exactly half the area. □

I find it interesting to notice that the theorem remains true even for zigzag patterns involving infinitely many zigs and zags. There is no need in the argument to assume that there were only finitely many triangles.

Read more in the book itself:

See also the supplement: